最近,整个数学界最轰动的新闻是,**数学家张益唐再次宣布获得重大成果,在朗道-西格尔(Landau–Siegel)问题上取得突破。呃,这话的前一句很容易理解,后一句就完全不知所云,朗道-西格尔问题是啥?

张益唐
实际上,这个新闻对我来说完全不意外。因为我2019年介绍张益唐时(),就提到过他在研究朗道-西格尔零点猜想(Landau-Siegel Zeros conjecture),而且对此很有信心。因此,最近的新闻完全在我的意料之中。
不过我以前并没有调研过朗道-西格尔零点猜想具体说的是啥,现在既然他说他做出来了,我就赶快做了一番调研。然而调研的结论是,这东西完全无法向普通观众解释。虽然我以前给大家讲解过很多硬核的数学问题,但这次真的是太硬了。就像《是,首相》里的经典台词:The Russians are too strong.
然而,我可以向大家解释清楚这事的背景。你如果了解这些,你的知识水平就超过了90%的人。
首先,最基本的问题是,张益唐是谁?其实张益唐现在已经非常有名了,他是数学界少有的饱经磨难、大器晚成的代表。
张益唐1955年出生于上海,1978年进入北京大学数学系读本科,1985年到普渡大学读博士。1991年博士毕业后,由于导师不给他写推荐信,他无法在学术界找到工作,以至于沦落到打各种零工,才能维持得了生活这样子。他送过外卖,卖过炸鸡,还在快餐店当过会计,作过收银员等等。有时他没地方住,只能在车里过夜。

打工是不可能打工的
然而奇妙的是,他在这种环境下都没有放弃数学,仍然经常到图书馆去读代数几何和数论方面的期刊文章。1999年,在他的北大师弟、新罕布什尔州立大学数学系教授葛力明的帮助下,他终于在44岁时获得了一个学术界工作:到师弟的这个系担任临时讲师。

葛力明
2005年,张益唐50岁时,终于从临时讲师成为正式讲师,因为他的微积分讲得很好。按照正常的轨迹,他似乎会在这个位置上平稳地退休。
然而,命运的车轮在这时才开始转动。2013年,张益唐在58岁时发表了石破天惊的论文《质数间的有界距离》(Bounded gaps between primes),这是人类几百年来在孪生质数猜想(twin prime conjecture)上第一个实质性的进展。

《质数间的有界距离》摘要
什么是孪生质数猜想?这是一个可以用小学数学知识很容易讲清楚的问题,所以我们来好好解释一下。
最前面的几个质数是2、3、5、7、11、13、17等等,它们之间的间隔分别是1、2、2、4、2、4等等。显然,间隔1只会出现一次,即2和3之间,因为2后面就再也不会有偶的质数了。那么,间隔2会出现多少次呢?
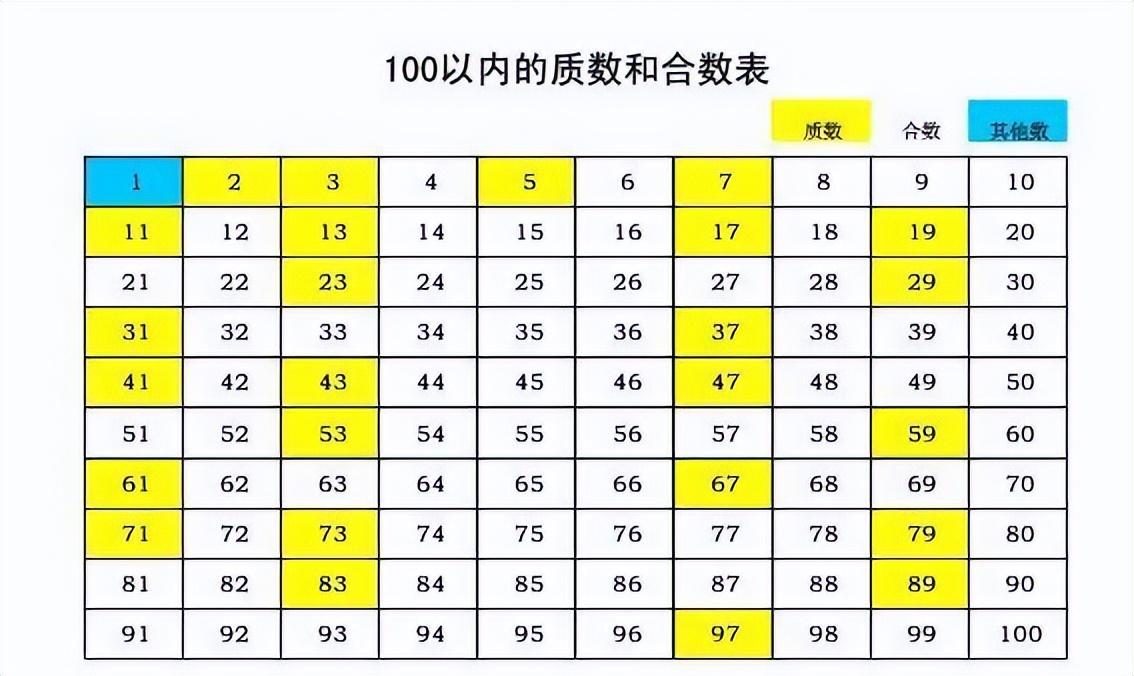
100以内的质数和合数表
一个惊人的猜想是:无穷多次!这就是孪生质数猜想。我们把一对相差2的质数称为孪生质数(twin primes),例如3和5、5和7、11和13。孪生质数猜想说的就是,存在无穷多对孪生质数。
实际上,随着自然数的增大,质数会变得越来越稀疏。也就是说,平均而言,相邻两个质数的间隔会变得越来越大。然而,孪生质数猜想说的就是,无论质数间隔变得多大,它总会在后面的某个地方突然缩小到2,这样的事会发生无数次。
目前,我们已知的最大的孪生质数对是:2996863034895 × 2^1290000 ± 1。这是两个大得惊人的数,写成十进制有将近40万位。
孪生质数猜想目前仍然是个猜想,也就是说我们还不知道它对不对,既没有证明也没有证伪。张益唐并没有证明孪生质数猜想,但证明了一个它的弱化版本。张益唐证明的是:存在无穷多对质数,它们的间隔不超过7千万。也就是说,无论质数间隔变得多大,后面总会在某个地方缩小到7千万或以下。假如把这里的7千万换成2,就是孪生质数猜想。
7千万这个数乍看起来很大,但实际上这是个重大的突破。因为在此之前人们并不知道出现无穷多次的质数间隔有没有上限,也就是说它完全可能是无穷大,即质数间隔变得越来越大,越来越大,不再缩小。张益唐的结果是第一次给出了一个有限的上限,即把无限变成了有限。无限和7千万之间是质的区别,7千万和2之间只是量的区别。现在明白这个成果为什么如此轰动了吧?
张益唐并没有完全挖掘他的方法的潜力。在他的论文发表后,立刻有很多数学家来改进。他们组织了一个合作项目“PolyMath8”来做这件事,包括菲尔兹奖获得者、著名华人数学家陶哲轩在内。

陶哲轩
通过这么多人的努力,目前这个上限从7千万缩小到了246。即我们已经证明了,存在无穷多对质数,它们的间隔不超过246。
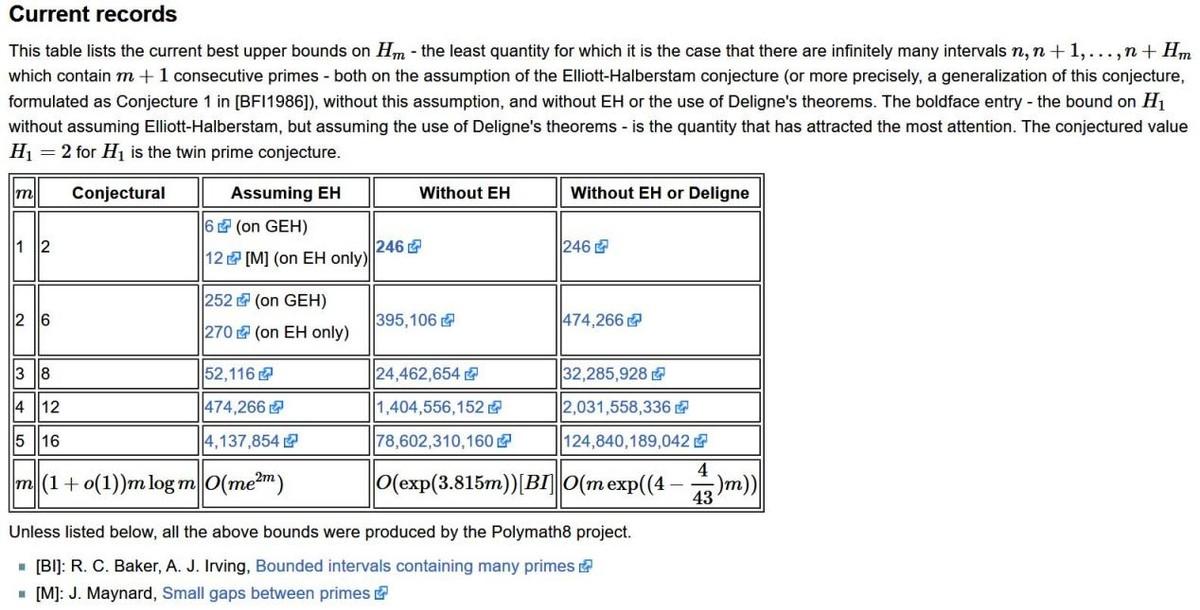
PolyMath8项目的当前纪录
这虽然也是不小的进步,但重要性显然不能和最初提出7千万相提并论。此外,这种方法的潜力似乎已经被挖掘殆尽,不足以从246缩小到2。如果想最终证明孪生质数猜想,应该会需要新的思想、新的方法。
在孪生质数猜想取得突破后,张益唐已经成为了一个传奇。但他并没有躺在功劳簿上,他又回到了一个他以前就经常深思的大问题,朗道-西格尔零点猜想。如前所述,我发现这个东西太复杂,无法向普通观众解释。
在这里只能稍微介绍一下背景。整个数学中有个最著名、最困难、也最重要的未解之谜叫做黎曼猜想(Riemann hypothesis),它是决定质数分布的关键。我以前做过六期节目解释黎曼猜想(),欢迎大家去看。
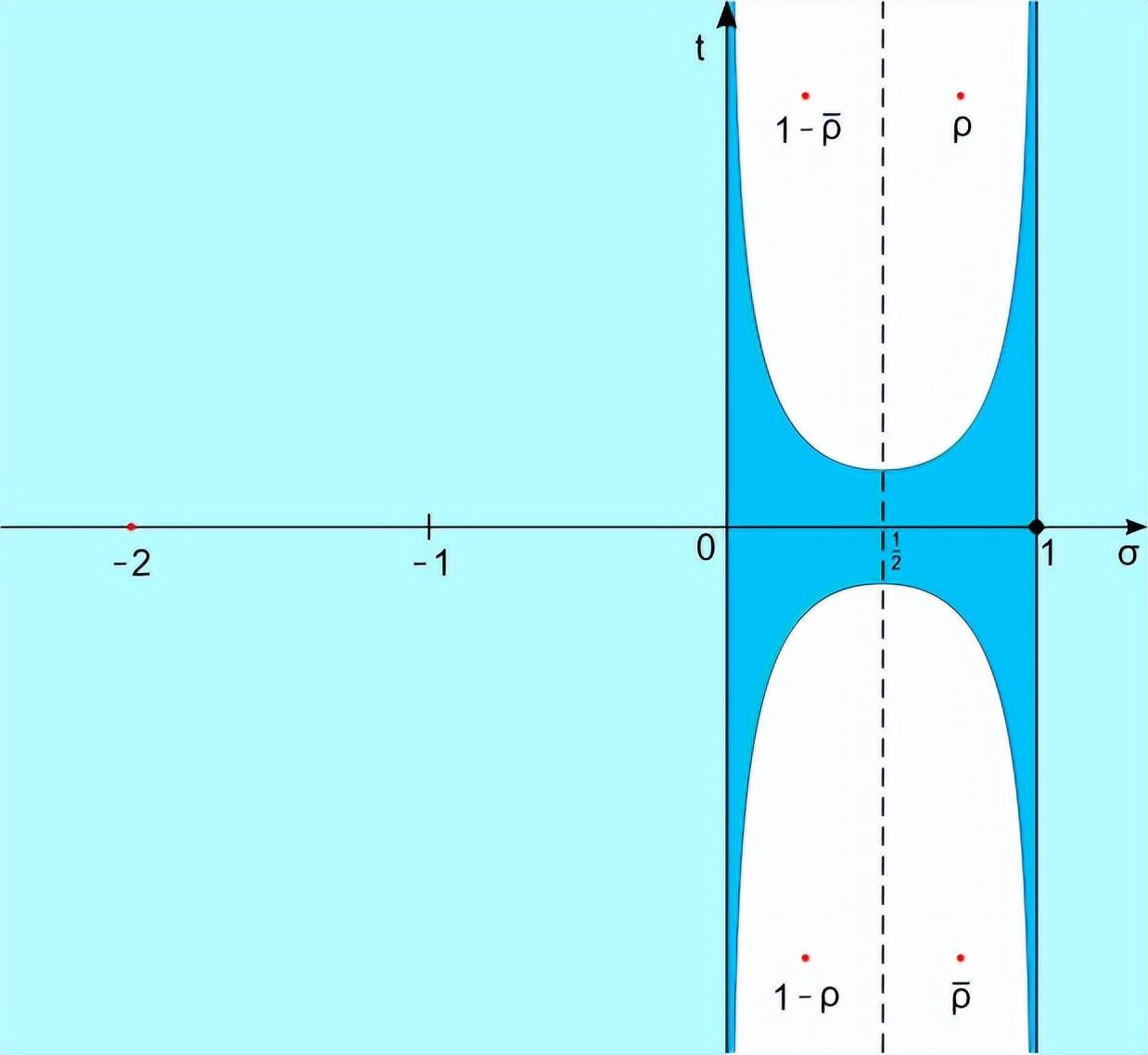
用复平面表示黎曼猜想:黎曼ζ函数的所有非平凡零点都在实部等于1/2的临界线上
黎曼猜想已经相当复杂了,但我觉得看了这六期节目以后,普通人还能理解个八九不离十。而朗道-西格尔零点猜想是一个以黎曼猜想为背景但更复杂的问题,所以我在这里就完全放弃了。大家只需要通过下面的叙述,了解这个问题的重要性就好了。

维基百科上朗道-西格尔零点的定义,如果你能看懂的话……
张益唐说:“对于数论学家来讲,有两个宇宙。在第一个宇宙里,不存在朗道-西格尔零点。但在第二个宇宙里,存在此零点。我们的困惑是,不知道我们到底生活在哪个宇宙里面。”
他的同事、数论学家Stopple解释说,如果张益唐能证明朗道-西格尔零点猜想,“就像是同一个人被闪电劈中两次”,“如果他从未成名,那么做出这项工作也会让他跟上次一样被世界瞩目”。
张益唐对自己能解决朗道-西格尔零点猜想充满信心,认为没有大的障碍,剩下的都只是技术性问题。英国数学大师哈代(Godfrey Harold Hardy,1877 - 1947)有一句名言:“比起其他任何艺术和科学,数学更是年轻人的游戏。”还有一句名言:“我从没见过哪个年过半百的数学家开创重大的数学进展。”

哈代
有人问张益唐如何看待哈代的这些观点,他的回答是:
“这个说法可能对我并不适用。我仍然相信我的直觉,我仍然对自己有信心。我仍然有不少愿景。”
目前,张益唐的论文《离散平均估计与朗道-西格尔零点》(Discrete mean estimates and the Landau-Siegel zero)刚刚发到网上,还没有正式投稿,所以还存在出错的可能性,要经过同行评审才有定论。如果它正确的话,张益唐就确实被闪电劈中了两次,在58岁做出一次奇迹后又在67岁做出另一次奇迹。只不过对普通人来说,这后一次奇迹比前一次难懂得多,所以我们没法用直观的语言来解释。

《离散平均估计与朗道-西格尔零点》摘要
虽然无法解读细节,我还是可以向大家解读一下这个成果的性质:跟前一次一样,在某个问题上取得了重大突破,但仍然没有解决问题本身。朗道-西格尔零点猜想说的是朗道-西格尔零点不存在,由此会导出一个直接的推论,某个量大于某个量的倒数即-1次方。

朗道-西格尔零点猜想的推论
张益唐不能证明这一点,但可以证明一个较弱的版本,把1换成2022。没错,真的是2022这个数,这个亮瞎眼的数不是在开玩笑!
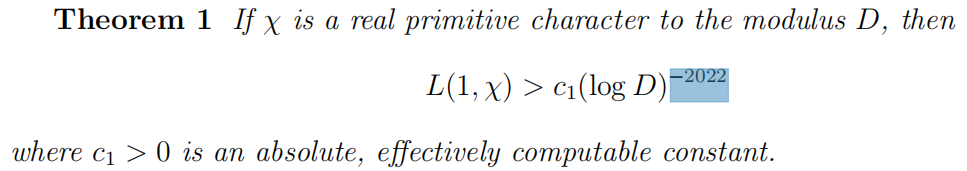
《离散平均估计与朗道-西格尔零点》定理1
张益唐在论文中也指出,2022这个估计很可能是可以改进的,就像对孪生质数猜想的7千万可以改进。但同时,不太可能通过目前的思路把2022改进到1,就像对孪生质数猜想无法把7千万改进到2。因此,这篇文章是对朗道-西格尔零点猜想的一个重大进展,但并不是完全解决。不过,张益唐的结果已经足以证明许多悬而未决的命题,把它们变成定理,因此这个成果确实是十分重大的。

张益唐对本文方法潜力的评估
我不久前介绍过,陈景润对哥德巴赫猜想的贡献也是这种性质()。目标是“1 + 1”,以前人们做的是“9 + 9”以至“1 + 3”等等,陈景润做到了“1 + 2”,只差一步但还差得很远。我想,能了解到这个程度,你的知识水平就超过了99%的人。

陈景润
最后我想说,即使看不懂这些数学细节,张益唐的奇迹仍然可以给我们巨大的鼓舞,告诉我们人永远都可以发挥主观能动性,永远都可以打破界限()。质数的最小间隔有上限,而人的奋斗没有上限。正如《三国演义》中,诸葛亮给周瑜的祭文中的一句话():
“始不垂翅,终能奋翼!”
